こんちは、Mathematica歴3年の筆者です。
当記事では超初心者向けにMathematicaの使い方を解説しています。
前回の記事ではMathematicaの基本操作について解説しました。
今回の記事では「For構文」についてわかりやすく解説したいと思います。
前回同様、具体的な課題を解決する過程でMathematicaを習得していきます。
1, 「 1から100までの整数の和」の計算
最初の課題は、前回と同じ「1から100までの整数の和」です。
こいつをFor構文を使用して解いていきたいと思います。
For構文とは繰り返し操作を行う構文です。
習うより慣れろということで、下図のように「 For[n = 1, n <= 5, n++, Print[n]] 」とセルに入力してShift + Enterを押してみて下さい。1から5までの整数が出力されれば成功です。

For構文では4つの引数を使用します。それぞれの役割は下図の通りです。
第1引数:nが何からスタートするか指定。これは専門用語で初期化と呼ばれます。
第2引数:実行条件をブール型で指定。上図のように書けば、何回繰り返すかを指定できます。
第3引数:nをどのように更新するかを指定。「n++」は「n = n + 1」や「n += 1」と同じで「nを+1する」という処理です。
第4引数:処理を記述。上図では「nを出力する」という処理をしています。
上図のコードでは、nを出力するという処理を5回繰り返しています。
ほとんどの場合、上図のようなFor[n=1, n<=”繰り返し回数”, n++, “処理”]の形で対処できます。この形を丸暗記しておいて下さい。
ではこのFor構文を使用して「 1から100までの整数の和」を計算してみましょう。
答えは何通りもあると思いますが、筆者は以下のコードを考えました。
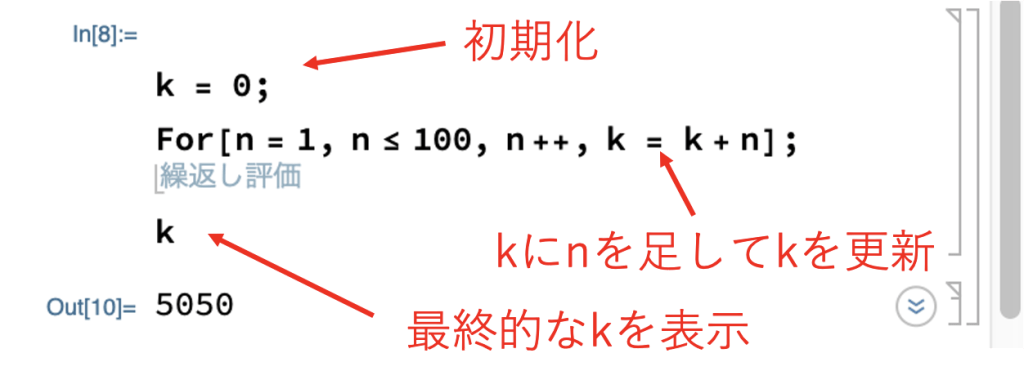
1行目の「k = 0;」で「k」を「0」に初期化しています。
2行目で「k」に「n」を加算する操作を100回繰り返しています。(ちなみに「k = k +n」は「k += n」とも書けます)
「なんで初期化する必要があるんだろう?」
という疑問をお持ちかと思います。実際、初期化をしないと正しい答えが得られません。
初期化の役割は主に2つあります。
1つ目は「型の宣言」です。Mathematicaでは関数の引数に正しい型を指定する必要があります。「kが整数型」であると宣言することで、関数の引数に指定した際のエラーを回避できます。(今回のコードでは、関数を使用していないため関係ないですが)
2つ目は「過去の記録の削除」です。今回の場合、上記コードを1回走らせると「k」に「5050」が記録されます。1行目の「k = 0」を消して、「k」を初期化をせずにもう1回コードを走らせてみて下さい。この場合「k = 5050」の状態から1から100までの整数が加算されるため、答えが「10100」となってしまいます。初期化によって過去の記録を削除することで常に正しい答えが得られます。
「じゃあ、どのタイミングで初期化が必要になるんだろう?」
と思ったかもしれません。これに関してはプログラミングの経験を積めば理解できるので、ひとまず初期化という操作があるという点だけは覚えておいて下さい。
2, 「 1から100までの整数で2021を割った時の最大の余り」の計算
次の課題は「 1から100までの整数で2021を割った時の最大の余り」です。
「Mathematica 余り」とグーグル検索をすると、Mod[”整数型”, “整数型”]で余りを計算できそうです。
「Mathematica 最大」とグーグル検索すると、Max[“リスト型”]でリストの要素で最大値を計算できることがわかります。

したがって、For構文を使用して2021で割った時の余りのリストを作成した後に、「Max」を使用して最大値を計算すれば良さそうです。
For構文でリストを作成する際には「AppendTo」という関数を使用します。「For」と「AppendTo」の組み合わせでリストを生成する操作は非常に多用しますので使い方を丸暗記しておいて下さい。
ひとまず筆者が作成した下図コードを見て下さい。なんとなく「Append」の使い方がわかると思います。

「AppendTo」を使用する際に重要なのが初期化です。上図では1行目で「list」を「空のリスト」に初期化しています。
「AppendTo」の第1引数は「リスト型」でないといけません。そのため、最初の初期化によって変数「list」が「リスト型」であると宣言しています。
また「AppendTo」は第1引数のリストの最後に第2引数の要素を追加していく関数です。この際、第1引数のリストは過去の記録を引き継いでしまうため、過去の記録を削除するために、最初にリストの中身を空に初期化する必要があります。
上図のコードでは、「n = 1」から始めて「n = 100」まで「2021をnで割った余り」を「list」に追加しています。
そして、出来上がった「2021を1から100までの整数で割った余りのリスト」の中から最大の要素を「Max」を使用して取り出しています。
3, 「 1から100までの整数で2021を割った時の余りの1の位の和」の計算
先程の作成した「 1から100までの整数で2021を割った時の余りのリスト」を使用して、「1の位の和」を計算してみましょう。
(「Sum」を使用すれば「For」を使用せずに解けますますが、せっかくですので「For」を使用して解きましょう。)
いつも通り使用する関数を探してみましょう。
筆者は「Mathematica 1の位」とグーグル検索して、下図のような「IntegerDigits」という関数を見つけました。

「IntegerDigits」は整数型を引数にして各桁の数字をリスト型で返す関数のようです。
したがって、「 1から100までの整数で2021を割った時の余りのリスト」の全ての要素に対して、「IntegerDigits」を使用して1の位を求めて加算していけば良さそうです。
ちなみに、「For」を使用してリストの全要素に対して何らかの処理を行う操作は頻出ですので、形を丸暗記しておいて下さい。
筆者の考えたコードは以下の通りです。

最初3行の余りのリストを作るコードは先程と全く同じコードですので説明は割愛します。
5行目の「For」によって「list」の全要素に対して1の位を取り出して「k」に加算しています。
新しく出てきたのは以下の2つです。どちらも超頻出ですので使い方を暗記してください。
・Length関数:リストを引数にしてリストの要素の個数を整数型で返す関数。「For」の中で「n<=Length[list]」と使用する形が超頻出。
・list[[m]]:「list」の「m」番目の要素を取り出す。Part関数の省略形。「-m」のように負の数を指定すると後ろから数えて「m」番目の要素を取り出す。超頻出。
「Length」はリストの要素数を数えてくれる関数です。上記コードのように「For」の第2引数で「n<=Length[list]」とすることで「list」の全要素に対して何らかの処理を行う形が頻出です。
また、「list[[m]]」と記述することで「list」の「m」番目の要素を取り出すことができます。「Part」関数の省略形です。わざわざ省略形が用意されているということは超頻出ということです。
上記コードでは「IntegerDigits[list[[n]]]」によって「list」の「n」番目の要素(整数型)の各位をリスト型に変換しています。そして「[[-1]]」によってリストの後ろから数えて1番目の要素、つまり1の位の数を取り出しています。
そして取り出した1の位の数を「k」に加算して答えを求めています。
第2回のFor構文の使い方は以上になります。
繰り返しますが以下の4つ形は必ず覚えてください。
・For[n=1, n<=”繰り返し回数”, n++, “処理”]の形
・「For」と「Append」でリストを作成する形
・「For」の中で「n<=Length[list]」と使用する形
・「list[[m]]」で「list」の「m」番目を取り出す形
第3回は「If文」について解説したいと思います。
「For構文」に加えて「If文」を使えるようになれば、ほとんどの処理をMathematicaで実装できます。
それではまたお会いしましょう!
