Mathematicaの使い方講座 ①基本操作

はじめまして、Mathematica歴3年の筆者です。

「Mathematicaを始めたいんだけど、何から手をつけていいかわからないなあ」

「最初に身につける基本は何？」

「いいチュートリアルが載っているサイトないかなあ？」

といった需要が筆者がMathematicaを始めるときにあったので、これからMathematicaを始める人向けにチュートリアルを作ってみました。

ターゲットは「今までプログラミングを全くやったことはないけど、これからMathemaricaを始めようとしている人」です！

全５回くらいで、Mathematicaを用いた「データ解析」や「シミュレーション」ができるようになることを目指します。

第１回目は「Mathematicaの基本操作」についてです。それではどうぞ。

私の記事では、具体的な課題を解決する過程でMathematicaを習得していきます。この方法が一番効率がいいからです。

そんなわけで、最初の課題は「1+1を計算すること」とします。

早速、Mathematicaを開いて上のタブから、「ファイル」→「ファイル」→「ノートブック」とクリックして下さい。

すると「名称未定義-１」というウインドウが立ち上がります。

この状態でEnterを押すと、下図のように「セル」と呼ばれるものが生成されます。

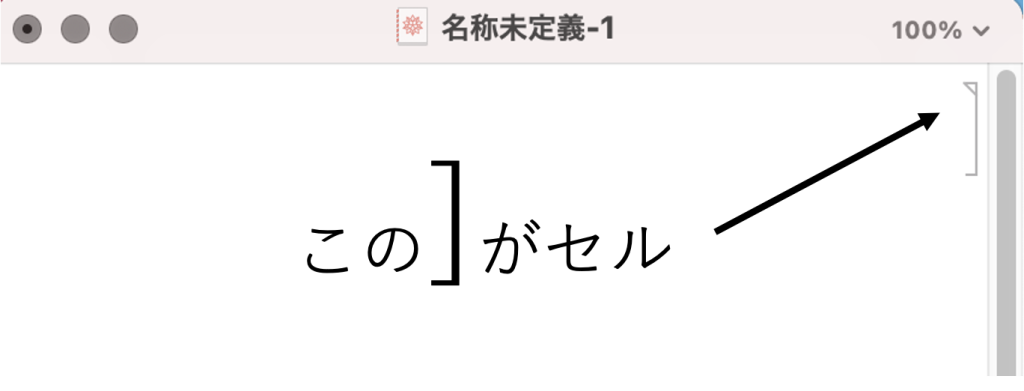
「セル」は日本語で例えるなら「段落」です。

Mathematicaでは、セルを選択した状態で「Shift + Enter」を押すことでセルの中のプログラムを実行します。

つまり、セルを分けることで小さく区切ってプログラムを実行できます。

「じゃあどこでセルを区切ったらいいんだ？」

とお思いかもしれませんが、セルを全く区切らなくてもプログラムは問題なく動くので、今は深く考えなくても大丈夫です。

では、セルの中に「1+1」と記述して「Shift + Enter」を押してみて下さい。

下図のように「Out[1] = 2」と表示されたら成功です。In[1]やOut[1]は仕様ですので特に気にしなくて大丈夫です。

ちなみに、引き算は「-」、掛け算は「*」、割り算は「/」、乗数は「^」になります。

次の課題は、「a = 1かつb = 2の時、a + bを計算すること」です。

「a + b」をセルに入力してShift + Enterを押しても計算できないのは直感的にわかるかと思います。

なぜなら、Mathematicaは「a」と「b」が何なのかを知らないのですから。

そこで先に「aは１」で「bは2」という情報を与えてから「a + b」を計算します。

下記のように１行目に「a = 1」、2行目に「b = 2」、3行目に「a + b」と記述してShift + Enterを押してみて下さい。

すると下図のように、１と２と３が出力されます。この出力はそれぞれ、１がaの値、２がbの値、３がa + bの値に対応しています。

しかしながら、今回の課題で知りたいのは「a + b」の答えである３だけであり、出力の１と２は目障りですよね。

そんな時のために、Mathematicaでは文末に「；」をつけることで、その行を出力しないようにできます。

試しに、下図のように1行目を「a = 1;」、2行目を「b = 2;」としてからShift + Enterを押してみて下さい。

3行目の「a + b」の答えである３だけが出力されます。

ちなみに「a = 1」は代入と呼ばれる操作です。

「a」は変数と呼ばれており、「=」を使うことで「変数a」に「整数1」を紐付け（代入）しています。

実はこの「=」は数学的な「等しい」とは意味が異なっています。

代入の「=」は「右辺を左辺に代入する」という意味です。

「結局、数学と一緒の意味じゃねえか！？」

という疑問をお持ちかと思います。

以下の例がわかりやすいかと思います。

1行目に「a = 1;」、2行目に「a = a+1」と記述してShift + Enterを押してみて下さい。

すると2行目の「a」の値である2が出力されます。

「=」を数学的な意味と捉えていると「a = a+1」は理解できないですよね。

説明すると、まず１行目で「変数a」に「1」を代入しています。

２行目では右辺の「a + 1」を先に計算して、その結果を「a」に代入しています。

結果、最終的に「a」に「2」が代入されるわけです。

ちなみに、筆者は「=」が代入であることを知らずに1年くらいMathematicaを使っていたので、すぐに理解できなくても大丈夫です。

数学の「=」とは違うんだなあくらいに知っておいて下さい。

さて、少し実践的な問題を解いてみましょう。

今回の課題は「1から100までの整数の和」です。

パッと思いつくのは「1 + 2 + 3 + ・・・・+ 100」と記述してShift + Enterを押すことです。ですが、この方法はもちろん今回はダメです。

そこで「関数」というものを使ってみたいと思います。

関数とは「平均を求める」や「合計値を求める」といった数学でよく行われる操作を簡単に記述する方法です。

例えば「平均を求める」という操作は「Mean」という関数によって簡単に実行できます。

実際に「１から５までの整数の平均」を「Mean」を使用して計算してみましょう。

１行目に「a = {1, 2, 3, 4, 5};」と記述して下さい。

これによって「変数a」に「１から５までの整数のリスト」が代入されます。

リストについては後で解説します。

次に２行目に「Mean[a]」と記述してShift + Enterを押して下さい。

３と出力されれば成功です。

「Mean」によって「リストa」の中身の１から５までの整数の平均が計算されます。

「関数が便利なのはわかったけど、たくさん関数を覚えないとMathematicaは使えないのか、、、、」

と思った方もいらっしゃるかと思いますが、ご安心ください。

実は関数を覚える必要は全くないのです。

なぜなら関数はググって使用するものだからです。

筆者自身もググらずに完璧に使用できる関数は10個くらいだと思います。

Mathematicaに限ったことではないですが、プログラミングではググるということが非常に重要です。

あなたが直面する問題のほとんどは、以前に誰かが直面して解決方法を考えてくれているものです。

わからないことがあったらすぐにググることを徹底して下さい。

先程の平均を求める関数は、「Mathematica　平均」とでもググれば簡単に見つけられます。

下図一番上の公式サイト（Wolfram言語ドキュメント）がわかりやすくまとまっています。

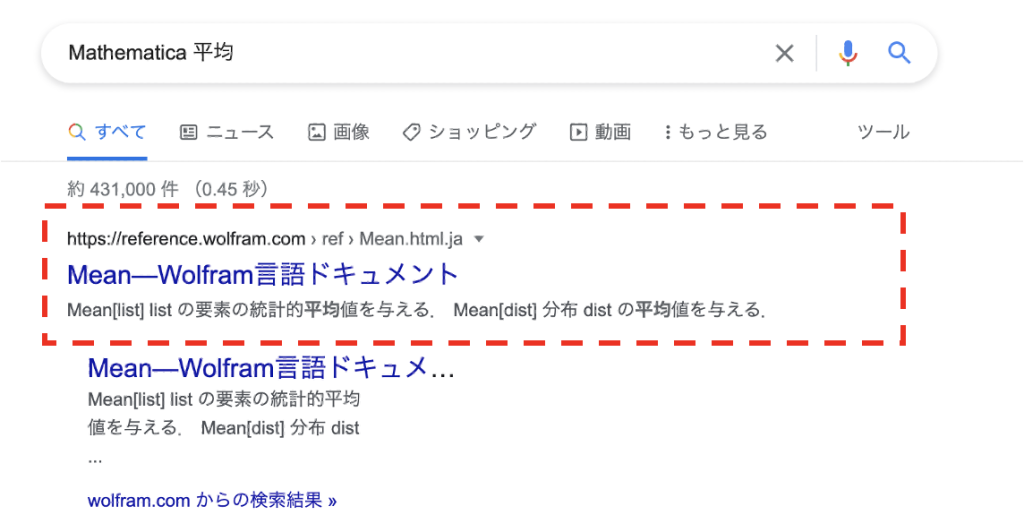
公式サイトをクリックすると、下図のように関数の詳しい解説が載っています。

特にわかりやすいのが、下にある「例」です。

公式サイトでは、「例」にあるコードをクリックするだけでコピーできる仕様になっています。

ですので、「例」の中で関係がありそうなコードを自分のセルにコピペして、必要な箇所だけ変更して使用するのがおすすめです。

さて、関数の説明に話を戻しましょう。Mathematicaの関数を使用する際には以下の3つのルールを守る必要があります。

先程のMean[a]がこの３つのルールを守っていることを確認しましょう。

ルール１とルール２に従って、「Mean」の先頭の文字は確かに大文字になっており、Meanの後ろには大括弧がついています。

ここで、ルール３の「適切な型」とは何だろうという疑問にお答えします。

Mathematicaでは変数を型として区別しています。

初心者が覚えておくべき型を以下に挙げます。

他にもいろいろな型がありますが、上の５つを意識して使い分けるだけで数値解析やシミュレーションまで実行可能です。

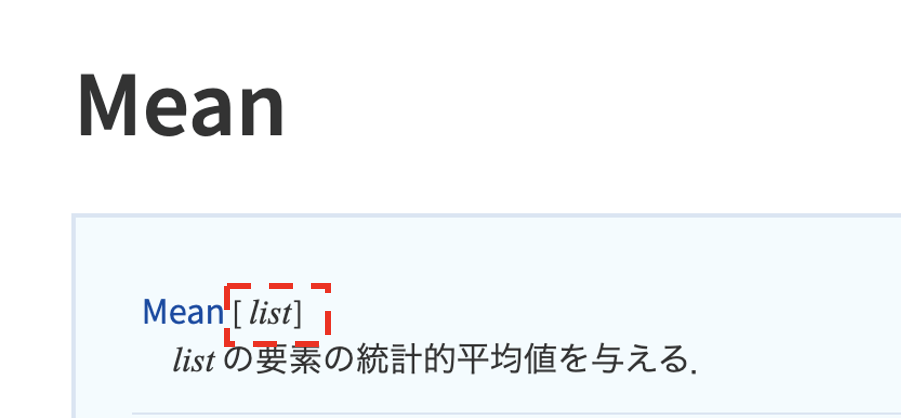
では、関数「Mean」の適切な型とは何でしょうか？

先程のググった結果をよく見ると、下記のように「list」（= リスト型）と書いてありますね。

そして「a」は「{1, 2, 3, 4, 5}」のリスト型でした。

したがってルール３も守られていることがわかりました。

ちなみに大括弧の中身を引数（ひきすう）と呼びます。

よく使う専門用語ですので覚えておいて下さい。

さて前置きが長くなりましたが、いよいよ「1から100までの整数の和」を計算してみたいと思います。

今までの話の流れから、おそらく以下の2つのステップで計算できそうですよね。

それぞれの関数をググってみましょう。

ステップ１においては、筆者が「Mathematica　等差数列」と検索したところ「Table」という関数を発見しました。

「Mathematica　Table」とググり直して、公式サイトに行って例を見ると以下のコードが使えそうでした。

このコードの「i^2」の部分を「i」にして、「10」を「100」に変更すれば良さそうですね。

実際に確認してみたところ、下図のように確かに「１から１００までの整数のリスト」を生成できていました。

次に、ステップ２の「リストの中身を合計する関数」を調べましょう。

筆者は「Mathematica　合計」とググりました。

すると「Total」という関数を見つけました。

「Total」は引数であるリストの合計を返す関数です。

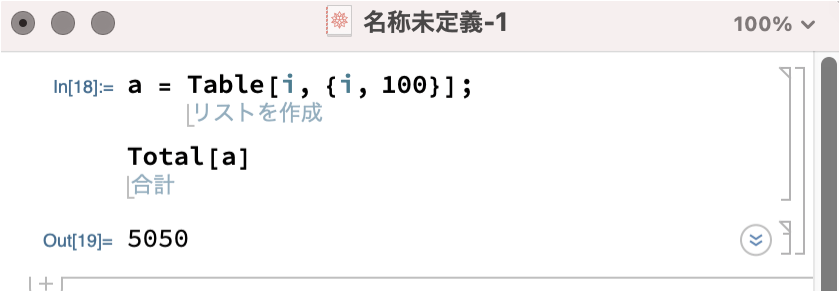
よって、先程の「１から１００までの整数のリスト」を「Total」の引数にすれば「１から１００までの整数の合計」を計算できるはず。

結果、下図のように答えが5050ということがわかりました。

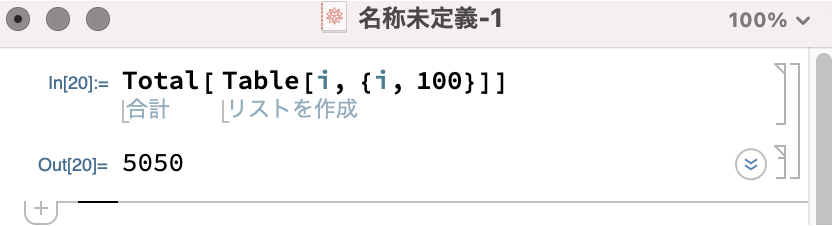
別の書き方として、下図のように「a」を使用しない書き方もあります。

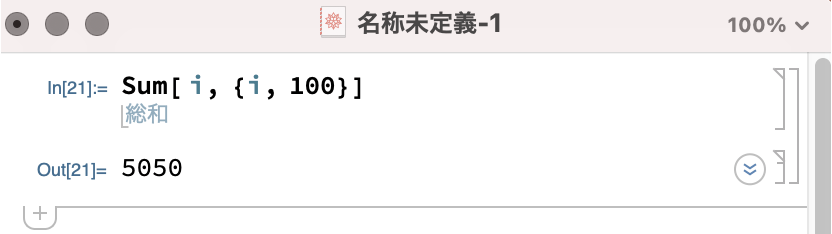
またググっている過程で「Sum」という関数を見つけました。この関数を使用すると下図のように計算できます。

このように色々な書き方がありますが、正直どれでもいいと思います。

数値解析やシミュレーションではコードが短いため、計算の速さはそれほど重要ではない場合が多いです。

とにかく初心者のうちは、コードが長くなろうが汚かろうがググって自分で書けるスキルを身につけることが重要です。

たくさんコードを書いていく過程で、速くて綺麗なコードが自然と書けるようになります。

長くなりましたが第１回はここで終了とします。お疲れ様でした

第２回は「For構文」と呼ばれる繰り返し処理を使って問題を解いていきたいと思います。