こんにちは、Mathematica歴3年の筆者です。
当記事では超初心者向けにMathematicaの使い方をわかりやすく解説しています。
前回の記事ではFor構文について解説しました。
今回の記事では「If文」について学んでいきたいと思います。
前回と同じく、具体的な課題を解決する過程でMathematicaを習得していきます。
1, 「 1から100までの整数で2021を割った時の最大の余り」の計算
最初の課題は前回と同じ「 1から100までの整数で2021を割った時の最大の余り」です。
前回は「AppendTo」と「Max」を使用して解きました。
今回は「AppendTo」と「Max」を使用せずに「If」だけを使って解いていきたいを思います。
筆者の考えたコードは以下の通りです。きちんと答えが「89」と求められました。
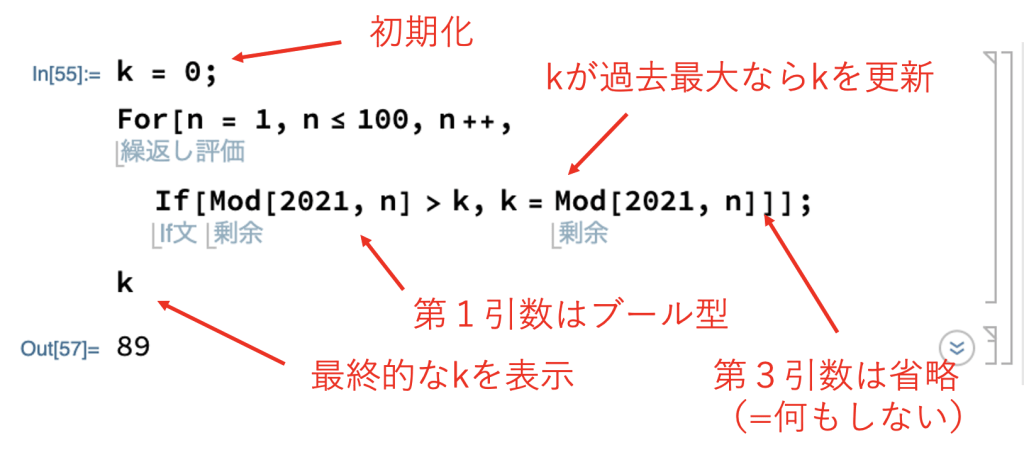
「If」は場合分けをしたいときに使用します。「〇〇〇の場合は〇〇〇の処理を行って、〇〇〇の場合は〇〇〇の処理を行う」といった具合です。
「If」を使用する際には3つの引数を指定します。
第1引数:ブール型(TrueまたはFalse)を記入して下さい。Trueの場合は第2引数の処理を行い、Falseの場合は第3引数の処理を行います。
第2引数:第1引数がTrueの場合に行いたい処理を記入して下さい。
第3引数:第1引数がFalseの場合に行いたい処理を記入して下さい。空欄でも大丈夫で、その場合何もしないです。
上図のコードでは第1引数に「Mod[2021, n] > k」というブール型を指定しています。
「>」や「>=」といった不等号を使用した不等式は、成立した場合にTrueを返し、成立しない場合はFalseを返します。
上図コードでは、「Mod[2021, n] > k」によって「今回計算した余りMod[2021, n] 」が「過去最大の余りk」よりも大きいかを判定しています。
そして第2引数に「k = Mod[2021, n]」という処理を指定しています。
これによって「今回計算した余りMod[2021, n] 」が「過去最大の余りk」よりも大きい場合、「過去最大の余りk」を「今回計算した余りMod[2021, n] 」に更新します。
結果として、最終的な「k」には「1から100までの整数で2021を割った時の最大の余り」が代入されているという仕組みです。
2, 「 1から100までの素数の和」の計算
次の課題は「 1から100までの素数の和」です。
いつも通り「Mathematica 素数」とグーグル検索して使えそうな関数を探してみましょう。
すると素数に関する公式サイトを発見できました。
使えそうな関数が並んでいますが、その中に素数かどうか判定する関数「PrimeQ」を見つけました。
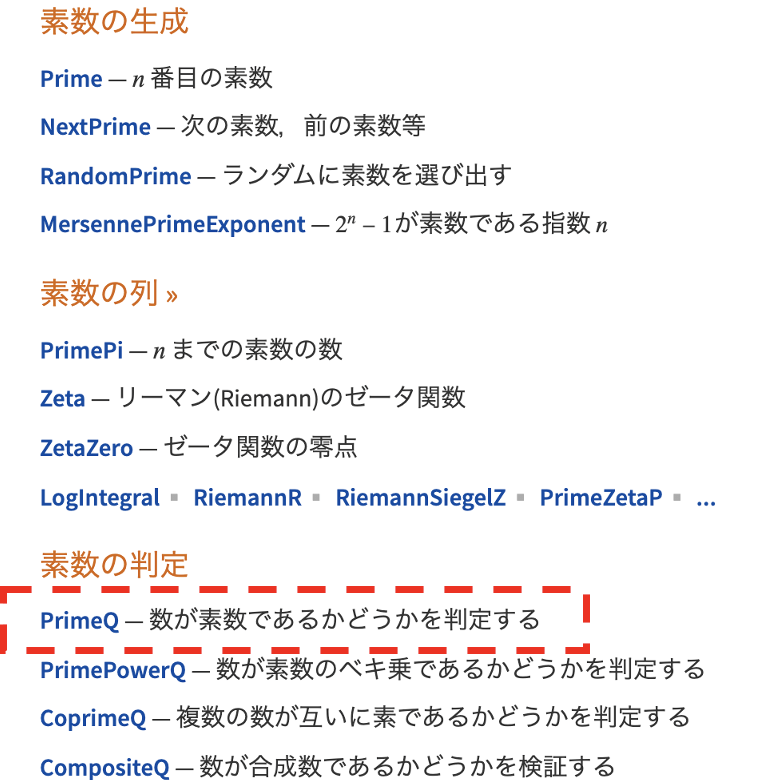
「PrimeQ」をクリックして使い方を見てみると、引数が素数ならTrue、引数が素数でないならFalseを返すと記載されています。

よって、1から100までの整数に対して「PrimeQ」を使用して素数かどうかを判定し、素数の場合は加算していけば良さそうです。
筆者が考えたコードは以下の通りです。
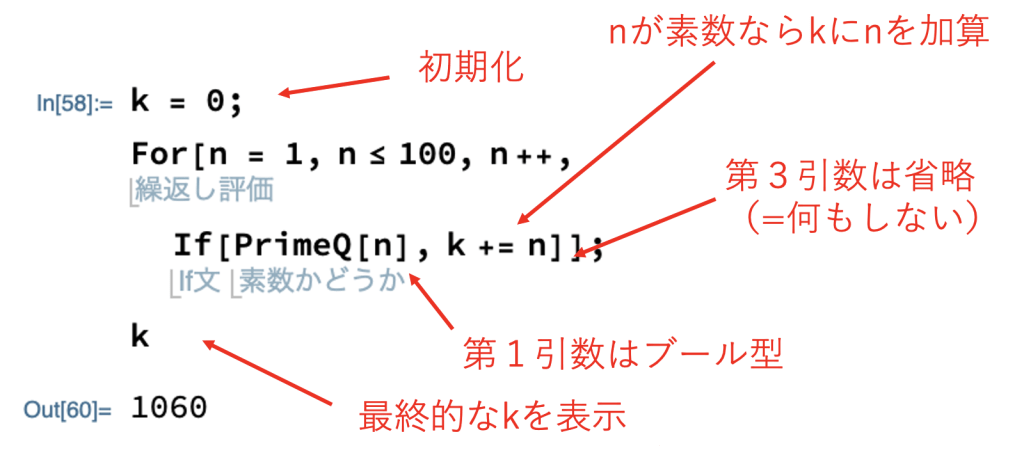
上記コードでは、いつも通り「k = 0」と初期化して、「k」の過去の記録を「0」にリセットします。
次に「If」を使って「PrimeQ[n]」が「True」なら「k」に「n」を加算しています。「k += n」は「k = k + n」の省略形です。
この操作を「n」が「1」から「100」まで繰り返し行うことで答えを求めています。
ちなみに「PrimeQ」を使用せずに以下のように解くことも可能です。

だいぶプログラミングらしくなってきましたね。
上記コードが理解できれば、Mathematica中級者といえるでしょう。
暗記事項は以下の3つです。
・Length関数:リストを引数にして要素の個数を整数型で返す関数
・list[[m]]:「list」の「m」番目の要素を取り出す。Part関数の省略形。
・“左辺” == “右辺”:「左辺」と「右辺」が等しい場合はTrueを返し、異なる場合はFalseを返す。
「Length関数」と「list[[m]]」は前回の記事でも登場しました。
「Length関数」と「list[[m]]」は、「For」を使用してリストの全要素に対して何らかの処理を行う際に頻出です。
また「”左辺”==”右辺”」と記述することで、「左辺」と「右辺」が同じかどうかをブール型で返します。
「==」も今後頻出ですので必ず覚えておいてください。
上記のコードでは、「primeList」に素数を追加していって、最後に「Total」で「primeList」の要素の和を計算しています。
素数かどうかの判定は、素数のリストである「primeList」の全要素に対して割り切れないかどうかで判定しています。
上記コードは、For構文の中にFor構文が入った構造になっています。この構造も頻出ですので、使い方に慣れておいて下さい。
ちなみに、For構文の第4引数は上記コードのように「;とEnter」を使って区切ることで複数指定できます。
ここでMathematicaの処理を強制終了する方法についても触れておきます。
今後複雑なコードを作ろうとすると、バグや計算量問題でMathematicaの処理が終了しない状況に必ず直面します。
筆者も先程のコードを作成している過程で、下図のように処理がいつまでも終了しない状況に直面しました。
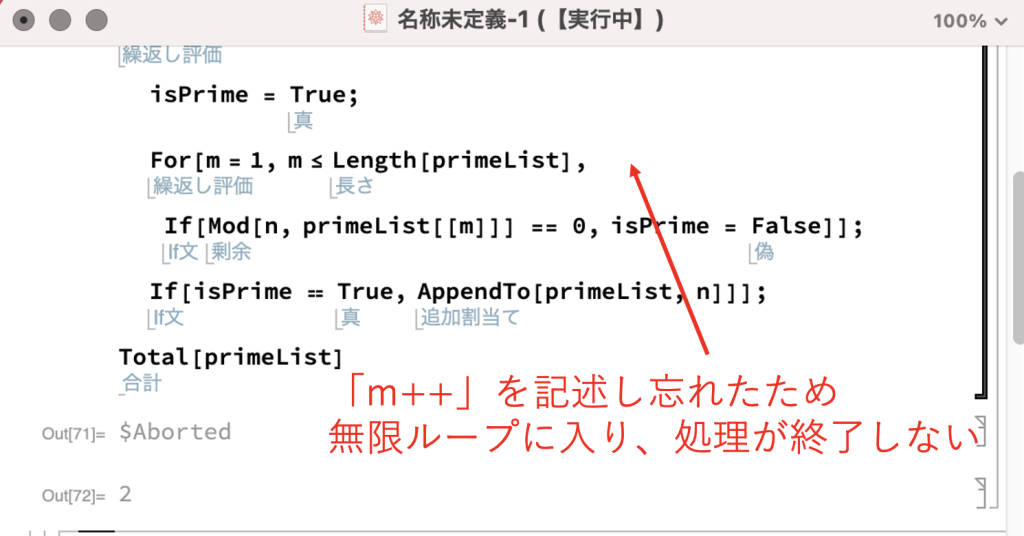
このような状況で計算を強制終了するには、下図のように1番上のタブから「評価」→「評価の放棄」を押して下さい。
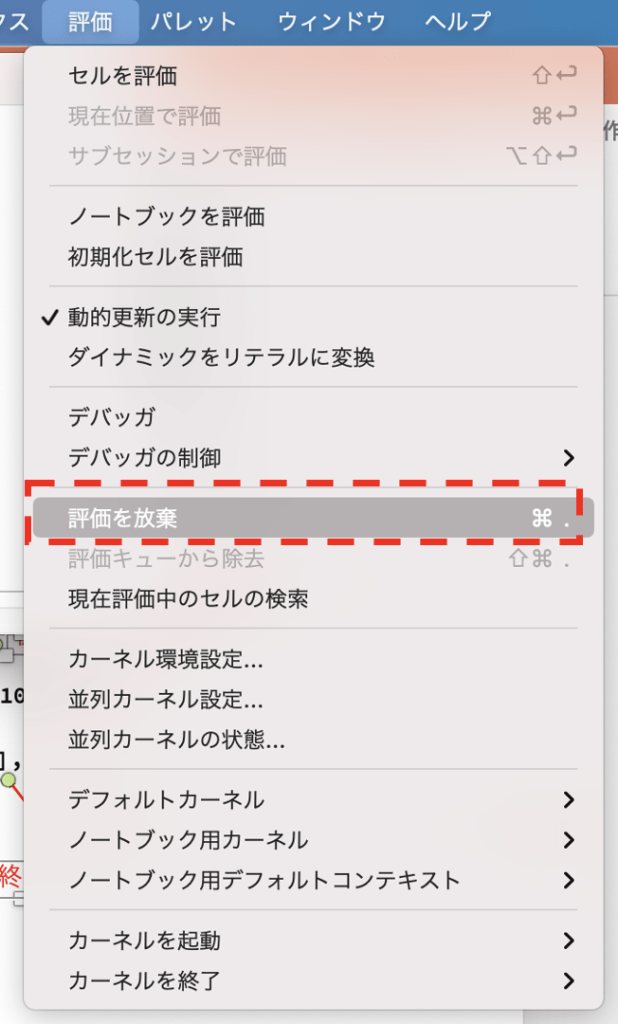
数秒で計算が強制終了されます。
この操作も今後多用するので覚えておいて下さい。
3, 「1から100までの整数のうち3の倍数であるが5の倍数ではない整数の数」の計算
次の課題は「1から100までの整数のうち3の倍数であるが5の倍数ではない整数の数」です。
「If」を使用して「3で割った余りが0」かつ「5で割った余りが0ではない」場合に「k += 1」とでもしてやれば良さそうです。
Mathematicaでは「かつ」や「または」といった論理式を記号で表現できます。
「Mathematica 論理」とグーグル検索すると関連した公式サイトを見つけられました。
頻繁に使用するものをまとめておきます。
・A && B:「AかつB」を表す。「A」と「B」が両方「True」の場合、「True」を返します。
・A || B:「AまたはB」を表す。「A」と「B」の少なくとも一方が「True」の場合、「True」を返します。
以上を踏まえて筆者が考えたコードは以下になります。
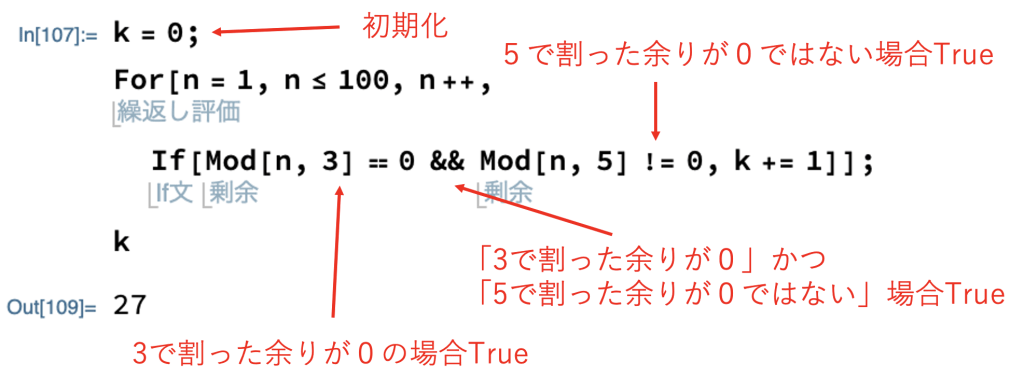
3行目の「==」は左辺と右辺が等しい場合「True」を返します。
同じく3行目の「!=」は左辺と右辺が異なる場合「True」を返します。
上記コードでは、「&&」を使用して「3で割った余りが0」かつ「5で割った余りが0ではない」場合に「k」に「1」を加えることで、該当する整数の数をカウントしています。
結果、最終的な答えは「27」と求まりました。
4, 「1から100までの整数のうち、いずれかの位に3を含む整数の数」の計算
次の課題は「1から100までの整数のうち、いずれかの位に3を含む整数の数」です。
使えそうな関数を探すと「IntegerDigits」という関数を見つけました。
「IntegerDigits」は整数を引数にして、各位の数字をリストで返します。
下図を見れば「IntegerDigits」の使い方が理解できると思います。

筆者が考えたコードは以下の通りです。

上記コードは「For」の中に「For」が入った構造になっています。
1番目の「For」の中で、1から100までの整数に対して「IntegerDigits」を使用して各位の数字をリストに変換して「list」に代入しています。
2番目の「For」の中で、「list」の全要素に対して「== 3」を調べて、少なくとも1つ「True」を返すならば「bool3」を「True」に切り替えます。
そして「bool3」が「True」の場合に「k+=1」とすることで、いずれかの位に「3」を含む整数の数をカウントしています。
ちなみに2番目の「For」で行っている操作は、「MemberQ」に置き換えることが可能です。
筆者は「mathematica リスト 含む」と検索して「MemberQ」を見つけました。

「MemberQ」は、第1引数のリストの中に第2引数の要素が含まれている場合に「True」を返す関数のようです。
つまり「MemberQ[list, 3]」と記述することで、「list」の中に「3」が含まれているかを調べることができます。
「MemberQ」を使用して解いたコードは以下の通りです。

先程と同じ答えが得られました。
今回のIf文の使い方は以上になります。
「For」に加えて「If」も使いこなすことができれば、Mathematicaでほとんどの処理を実装することが可能です。
次回はグラフの作り方について解説していきたいと思います。
