こんにちは、Mathematica歴3年の筆者です。
当記事では超初心者向けにMathematicaの使い方をわかりやすく解説しています。
前回の記事ではグラフの作り方について解説しました。
今回の記事では「フィッティング」について学んでいきたいと思います。
フィッティングとは、データを指定した関数形に当てはめてパラメータを算出することです。
当記事では非線形フィッテング、パラメータの算出、パラメータ誤差の算出、エラーバー付きグラフの作り方を解説します。
それではどうぞ。
1, 非線形フィッティング
最初に非線形フィッティングから解説していきたいと思います。
「線形フィッテングからではなくて非線形フィッティングから??」
とお思いではないでしょうか?
確かにMathematicaには、線形フィッテングと非線形フィッティングの2種類のフィッティング方法が存在します。
しかしながら、Mathematicaの非線形フィッテング関数「NonlinearModelFit」は線形フィッテングとしても使用可能です。
暗記事項を減らすという意味で「NonlinearModelFit」のみでフィッティングを行います。
早速、「NonlinearModelFit」を使用してデータをフィッティングしてみましょう。
使用するデータは、前回と同様に比例にノイズを加えたリストです。
私が作ったコードは以下の通りです。
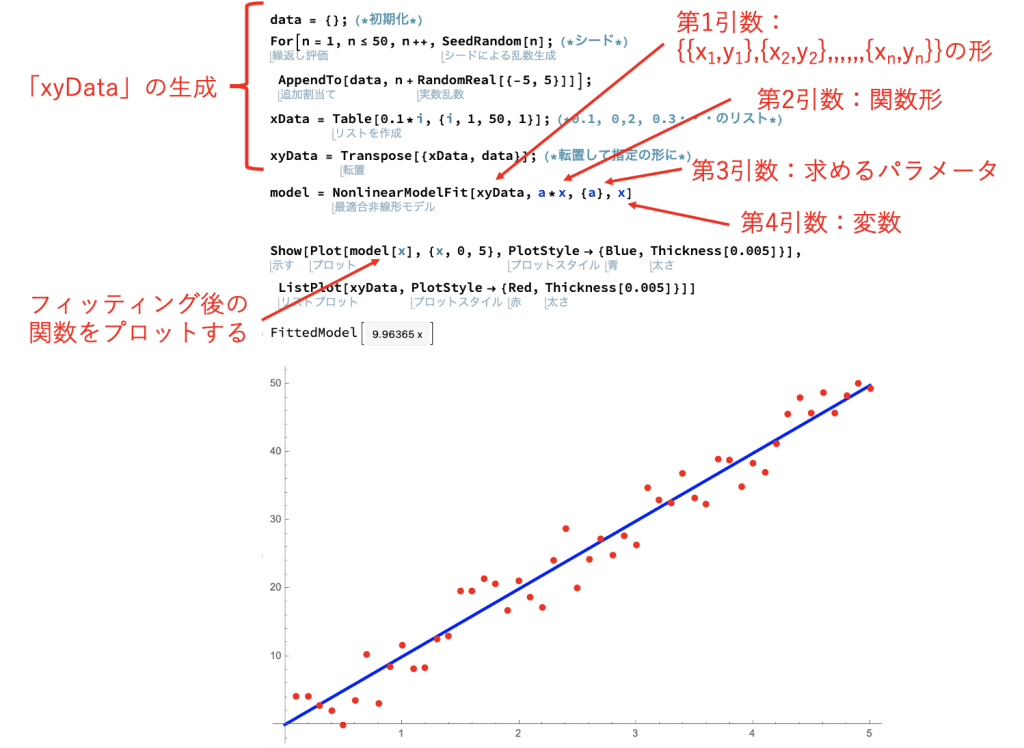
「NonlinearModelFit」の使い方はやや特殊ですので、テンプレを作って使い回すのがオススメです。
上図は、データ「xyData」を関数形「y = ax」でフィッティングするコードです。
まず、「NonlinearModelFit」の第1引数にフィッティングに使用するデータ「xyData」を指定します。
データの形は「{{x1, y1}, {x2, y2},,,,,{xn, yn}}」の形で指定して下さい。
第2引数には関数形である「ax」、第3引数には求めるパラメータのリスト「{a}」、第4引数には変数「x」を指定しています。
「NonlinearModelFit」を使用する際にはパラメータが空であることに気をつけて下さい。
Mathematicaでは、文字の色が青色ならパラメータが空ということになります。
上記コードを実行してみてもしエラーが出た場合、パラメータ「a」に何らかの値が代入されてしまっていないか確認してみて下さい。
もし「a」に何らかの値が代入されてしまっている場合、「NonlinearModelFit」の引数で「a」がパラメータとして認識されないためエラーとなります。
このような場合、セルの最初の行に「Clear[“Global`*”]」と記載すると解決できます。「Clear[“Global`*”]」は全ての変数を空に初期化してくれます。
上記コードをエラーなく実行できたら、最適なフィッティング関数は「y = 9.96365x」と求まります。
次に、このフィッティング関数とデータのリストをまとめて表示して、フィッティングがどの程度うまくいったのかを可視化してみましょう。
Mathematicaに限ったことではないですが、フィッティングを行なった際は必ず目視でフィッティングがうまくいっているか確認して下さい。
目視でフィッティングの良し悪しを判断する際には、前回解説した通り「Show」を使用することがオススメです。
「Show」を使用することでフィッティング関数とデータのリストをまとめてひとつのグラフに表示することができます。
「Show」の第1引数の「Plot」で「NonlinearModelFit」で作成したフィッティング関数を表示しています。この部分を簡単に説明しますと、「NonlinearModelFit」で作成した関数を「model」という変数に代入した後に、「Plot[model[x], {x,0,5}]」と記述してやることで、「xが0から5 の範囲」で「NonlinearModelFit」で作成した関数を表示しています。
2, 初期値と制約条件付きのフィッティング
続いて「初期値と制約条件付きのフィッティング」を行なってみましょう。
複雑な関数形のフィッティングでは、初期値や制約条件をうまく指定しないとうまくフィッティングできない場合が多いです。
そこで、適当な初期値や制約条件をつけてフィッティングを行う方法を身につける必要があります。
試しに「y = a * exp(x/b) + c」の関数形を使用して、初期値が「a = 1, b = 40, c = 1」で「a > 0」かつ「x = 0の時、y = 1」という制約条件下でフィッティングを行なってみましょう。
答えとなる関数は「y = 0.5 * exp(x/50) + 0.5」としました。
サンプルコードは以下の通りです。
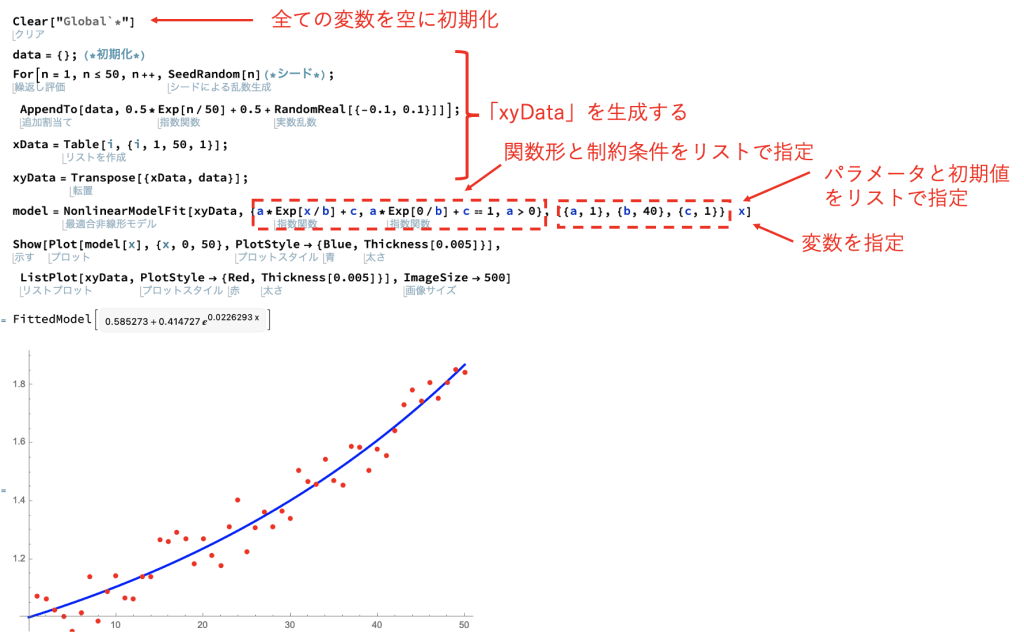
上記コードは汎用性が高いため、コピペできる形で載せておきます。フィッティングを行う際のテンプレとして使用して下さい。
上記コードを説明いたします。
まず1行目で「Clear[“Global`*”]」によって全ての変数を空に初期化しています。
2〜4行目で、関数「y = 0.5 * exp(x/50) + 0.5」に対して、「x」が「1」から「50」まで代入した値それぞれ「-0.1」から「0.1」の乱数ノイズを加えた値を「data」に格納しています。
5〜6行目で「Transpose」を使用して「data」と「xData」を転置して、「NonlinearModelFit」で使用可能な形の「xyData」を生成しています。
7行目の「NonlinearModelFit」の第1引数にフィッティング対象データである「xyData」を指定しています。第2引数には関数形「a*Exp[x/b] + c」と制約条件「a*Exp[0/b] + c == 1」および「a > 0」を指定しています。第3引数にはパラメータの初期値「a = 1, b = 40, c = 1」を「{{a, 1}, {b, 40}, {c, 1}}」の形で指定しています。第4引数には変数「x」を指定しています。
8〜9行目で、先程と同様にフィッティングした関数とデータのプロットをまとめて表示しています。
3, パラメータ誤差の表示
フィッティングを行なってパラメータを算出した際にしばしば議論になるのが「パラメータの誤差はどの程度か?」ということです。
パラメータ誤差を算出するためには、残差から算出した標準偏差をデータ点数の平方根で割って、、、、などのやや煩雑な計算が必要になります。
しかし、Mathematicaでは簡単にパラメータ誤差を算出することできます。
先程作成した「model」をそのまま使用して、新しいセルに「model[“ParameterErrors”]」と記述してShift + Enterで実行してみて下さい。
下図のように「a, b, c」の標準誤差がリスト型で取得できます。(赤文字で忠告が出ていますが気にしなくて大丈夫です。)

ちなみに「a, b, c」の値は下図のように「model[“BestFitParameters”]」で取得できます。

「model[“BestFitParameters”]」の中身を見てみると、何やら「→」が入った形になっていますね、、、、「→」は「Rule」と呼ばれるもので「/.」で表される「ReplaceAll」と併用されることが多いです。
ごちゃごちゃ説明するよりも公式サイトに載っていた下記のコードを見ていただくと「→」と「/.」の使い方を理解できるかと思います。

上図では、「→」と「/.」を使用してリストの全要素に対して「x」の部分を「1」に置き換えています。
この書き方に基づくと、「model」の中から「a, b, c」を取り出すためには以下のように記述すればよいです。

ちなみに「→」はMathematica上では「->」で入力できます。
さてここまでで、「model」からパラメータとその誤差を取り出すことができました。
最後にパラメータとその誤差を「±」をつけて表示してみましょう。
使用する関数は「Around」です。「Around」は第1引数と第2引数に対して「第1引数±第2引数」の形で不確かさを持った値を返します。
この「 Around」を使用して「model」の中のパラメータ「a, b, c」を「パラメータ±誤差」の形に直すコードは下記の通りです。
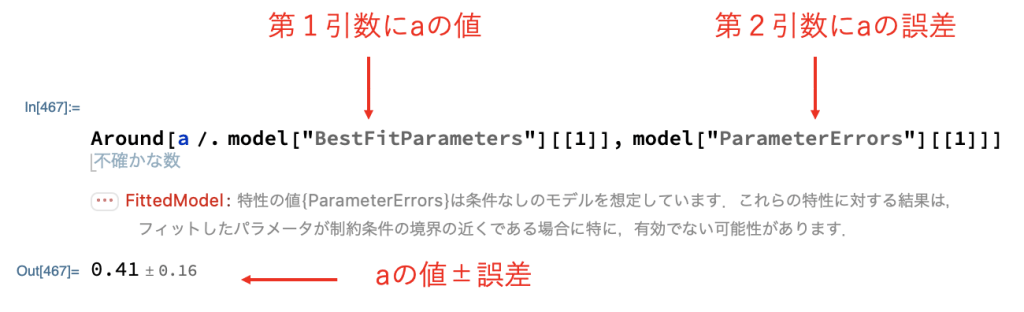
「Around」を使用することで、確かに「パラメータ±誤差」の形に変換できていますね。
実は、この「パラメータ±誤差」を「ListPlot」の引数で使用することでエラーバー付きのグラフを作ることができます。
4, エラーバー付きグラフ
最後にエラーバー付きのグラフを作成してみましょう。
試しに「xyData」のノイズに対してパラメータの値と誤差がどのように変化するのかを調べてみましょう。直感的にノイズを増やすと誤差が大きくなるはずです。
実際に横軸をノイズ、縦軸をフィッティングで求めた「a」、エラーバーを「aの誤差」とした折線グラフを作成します。
コードは以下の通りです。

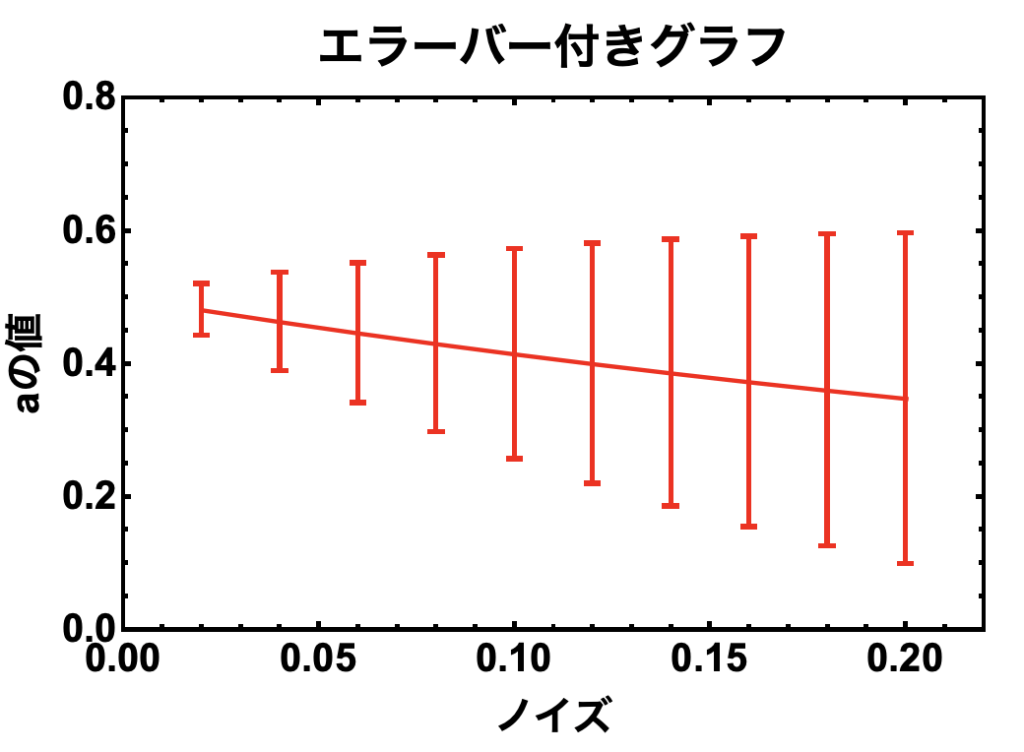
コピペ用のコードは以下の通りです。
コードの中身を簡単に説明いたしますと、「a±誤差」のリストである「aList」、およびノイズのリストである「noiseList」を生成し、「ListPlot」で出力しています。
ノイズは5行目の「noise = 0.02*m」で定義されています。「m」を1から10まで繰り返し処理して「noiseList」に「0.02, 0.04, 0.06,,,,」が格納されています。
あとはこれまでと同様の手順で「NonlinearModelFit」を使用してパラメータ「a」とその誤差を算出し、「Around」を使用して「a±誤差」の形に変換して「aList」に格納しています。
最後に、作成した「aList」と「noiseList」を転置して「ListPlot」で使用可能な形に変換して表示しています。
このように「ListPlot」の引数として「a±誤差」の形を指定すると自動でエラーバーを表示してくれます。便利!!!
第5回「フィッティング」はここで終了とします。お疲れ様でした。
第6回は「乱数シミュレーション」について解説します。
当記事をお読みいただきありがとうございました。
