こんにちは、Mathematica歴3年の筆者です。
当記事では超初心者向けにMathematicaの使い方をわかりやすく解説しています。
前回の記事では「フィッティング」について解説しました。
今回の記事では「乱数シミュレーション」について学んでいきたいと思います。
乱数シミュレーションとは、乱数を使用して行うシミュレーションのことで、別名モンテカルロシミュレーションとも呼ばれています。
当記事では、乱数に従って直線上を移動する「1次元のランダムウォークシミュレーション」から始まり、乱数に従って平面上を移動する「2次元のランダムウォークシミュレーション」までを解説します。
それではどうぞ。
1次元のランダムウォークシミュレーション
まず1次元のランダムウォークシミュレーションを行なってみましょう。
条件は以下の通りです。
・1秒毎に1/3の確率でx軸上を-1, 0, +1だけ移動する。
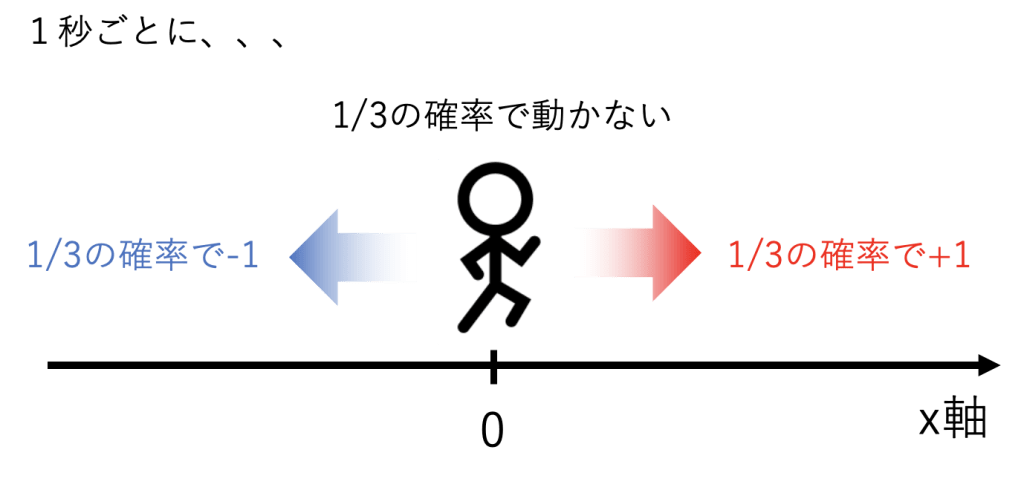
以上のようにx軸上を移動する人の100秒後の位置を10000回測定してみましょう。
1秒ごとにどう移動するかを乱数を用いてシミュレーションします。
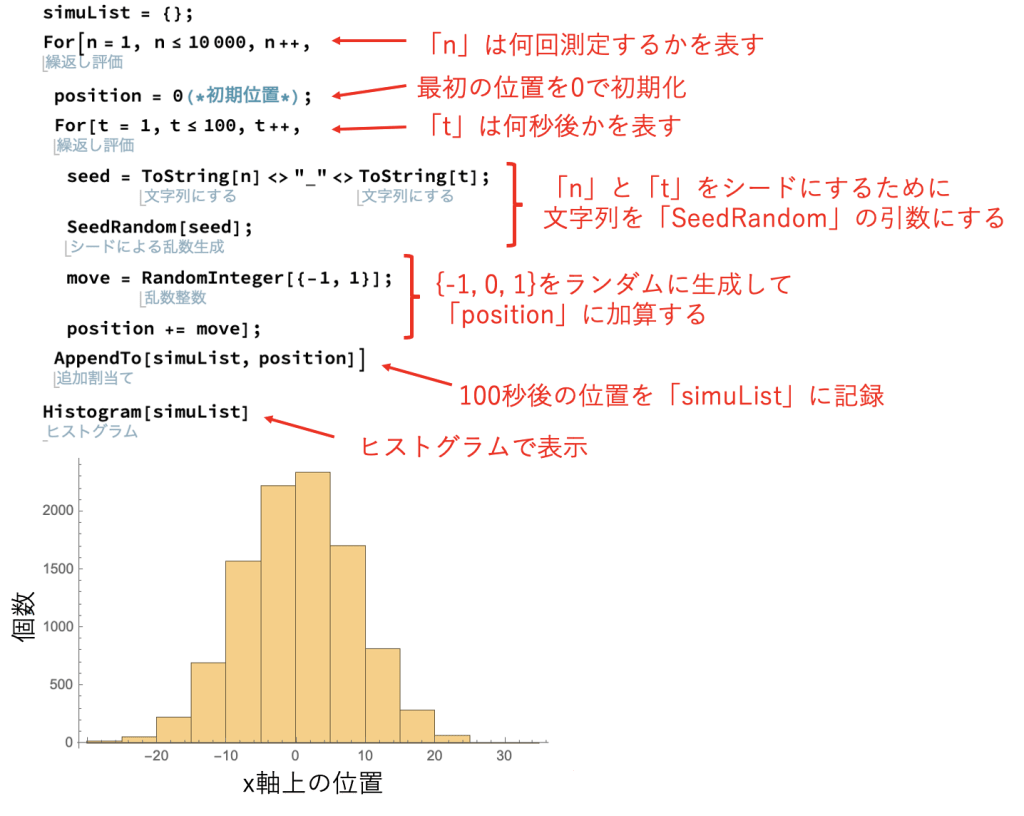
筆者の作ったコードは以下の通りです。
上記コードは以下でコピペできます。
上記コードを解説いたします。
1行目で、100秒後の位置のリスト「simuList」を空に初期化しています。
2〜9行目は、測定回数である「n」回繰り返すFor構文です。
3行目で、最初の位置「position」を「0」に初期化しています。
4〜8行目は、測定時間である「t」回繰り返すFor構文です。
5〜8行目では、「n」と「t」をシードにして「{-1, 0, 1}」の中から等確率で数値を取得して位置「position」に加算しています。
ここで新しく「ToString」と「<>」を使用しました。この2つについて解説いたします。
ToString:引数を文字列型に変換する関数。例えば「n = 1」の時、「ToString[n]」とすると出力は文字列型の「”1″」となる。(「”n”」とすると出力は「”n”」となってしまう。)
<>:文字列型を結合する時に使用する。例えば、「n = 1」かつ「t = 2」の時、「ToString[n] <> “_” <> ToString[t]」と入力すると、出力は文字列型の「”1_2″」となる。
上記コードでは、「ToString」を使用して「n」と「t」を文字列型に変換した後、「<>」を使用して文字列を結合して「SeedRandom」の引数に設定しています。これによって、「n」と「t」のどちらかが変化すれば、異なるシードから乱数を生成できるという仕組みです。
10行目で、作成したx軸上の位置のリストをヒストグラムで表示しています。結果、100秒間移動させても、ほとんどが原点付近にいることがわかりました。
さて、今回のランダムウォークシミュレーションで位置の2乗は時間に比例することが知られています。
(先程調べた100秒移動後の位置がほとんど原点であることを考えると、位置の2乗が時間に比例するというのは不思議だと筆者は思いますが、、、、)
実際にシミュレーションで確認してみましょう。
まず、横軸を時間t、縦軸をx軸上の位置としたグラフを作ってみます。
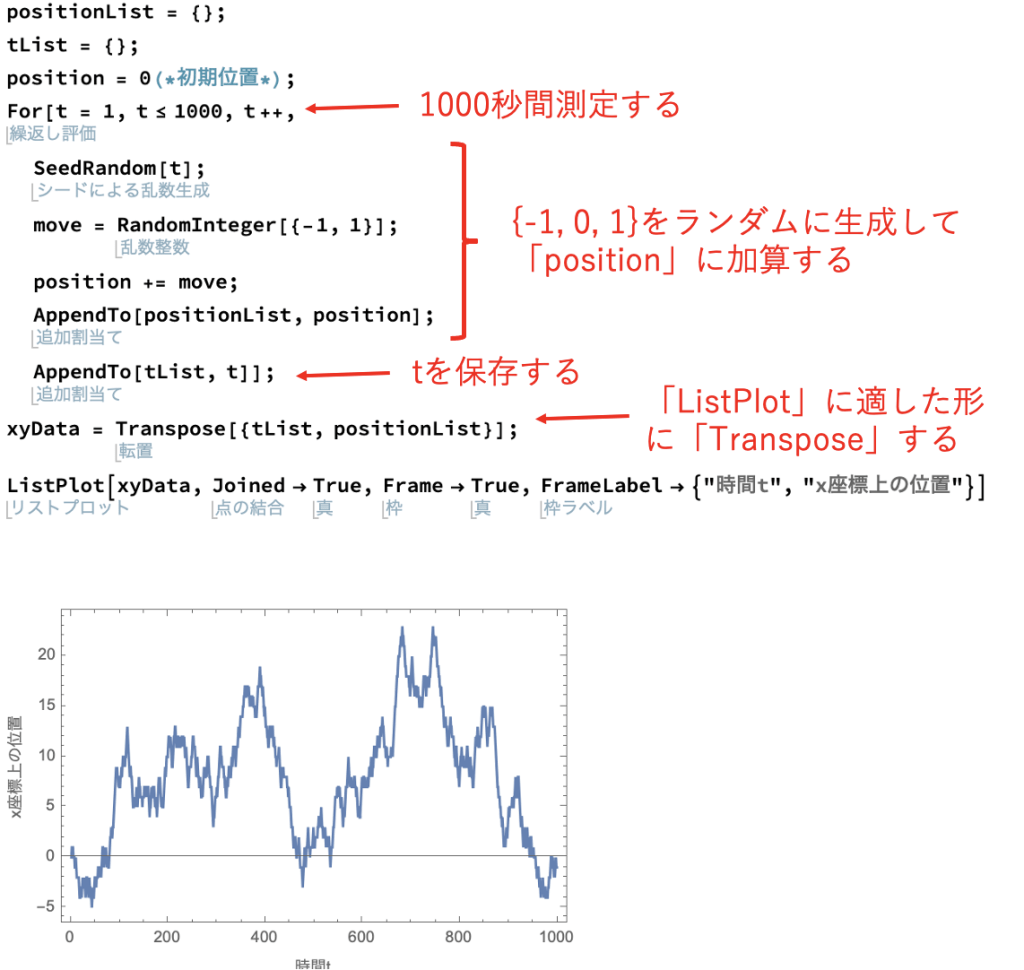
コピペ用は以下です。
このグラフをもとに、横軸をt、縦軸をt秒間の移動距離の2乗としてプロットしてみましょう。
ここでちょっとした工夫をしてみます。
一例として200秒間の移動距離の2乗を計算してみましょう。パッと思いつくのはt = 0からt = 200までを使用した移動距離の2乗ではないでしょうか。
しかしよく考えみると 、200秒間の移動距離の2乗はt = 1からt = 201までの移動距離の2乗でも良いですし、 t = 500からt = 700までの移動距離の2乗でも良いですよね。
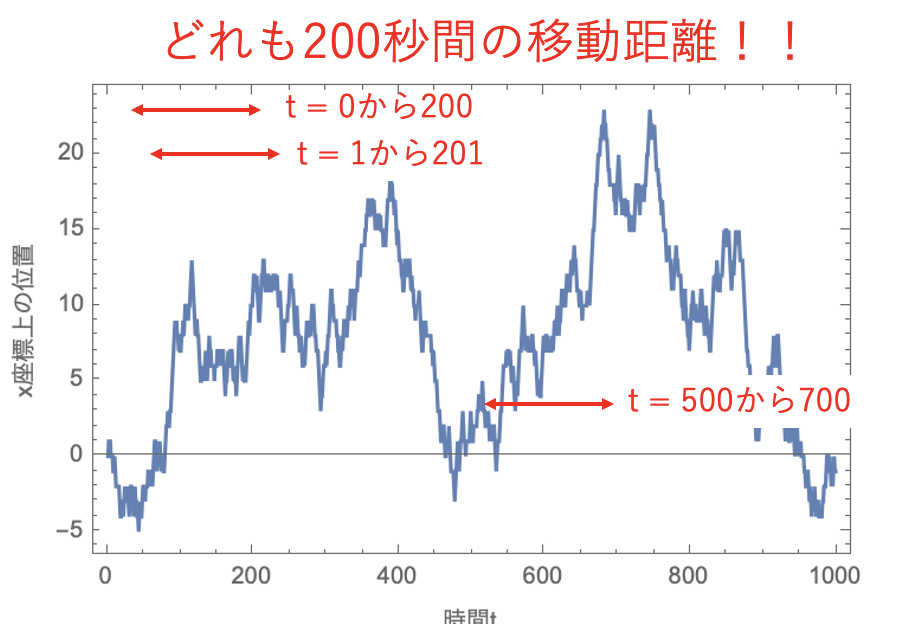
上図のようにtの測定開始をずらすことで1つのグラフから様々な移動距離の2乗を計算できます。
そしてこの様々な移動距離の2乗の平均を取ったものをMSD(Mean Square Displacement)と呼びます。
実際に時間tに対してMSDをプロットしてみましょう。理論上は直線になるはずです。
私の作ったコードは以下です。
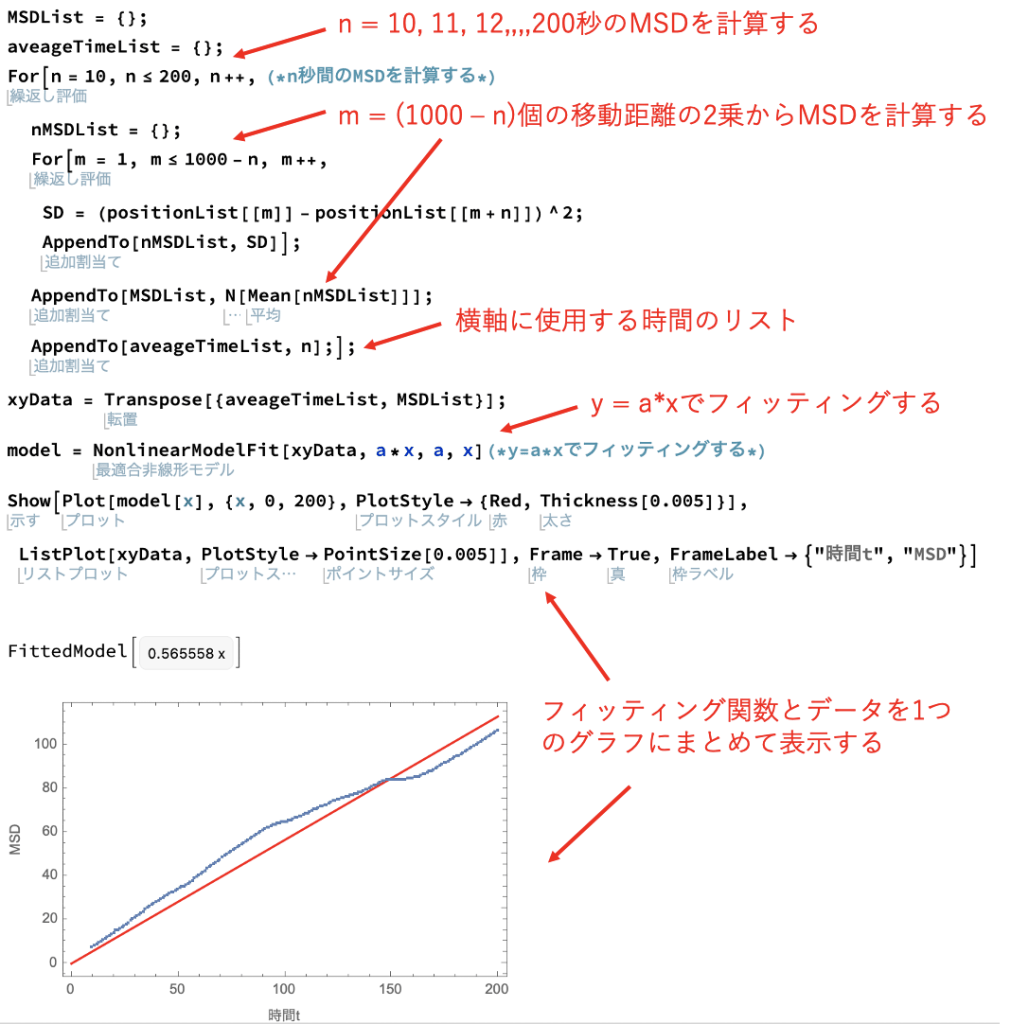
コピペ用は以下です。
上記コードでは10, 11, 12・・・200秒のMSDを計算しています。
そして、10, 11, 12・・・200秒のMSDを線形関数「y = ax」でフィッティングして、データとまとめて1つのグラフに表示しています。
上図のグラフを見てみると、確かにMSDが時間に対して比例していそうですね。
また、「y = ax」でフィッティングして傾き「a」を算出したところ「a = 0.565558」と求められました。この「a」は拡散係数と呼ばれる値と関連してます。
この辺の理論は既に詳しく研究されており、この記事がわかりやすくまとまっています。ぜひご一読ください。
ひとまず、1次元のランダムウォークシミュレーションをMathematicaで実装できました!!
2次元のランダムウォークシミュレーション
続いて2次元のランダムウォークシミュレーションを行ってみましょう。
条件は以下の通りです。
・1秒毎に1/3の確率でx軸上を-1, 0, +1だけ移動する。
・1秒毎に1/3の確率でy軸上を-1, 0, +1だけ移動する。
1000秒間の移動の様子をグラフに表すコードは以下の通りです。
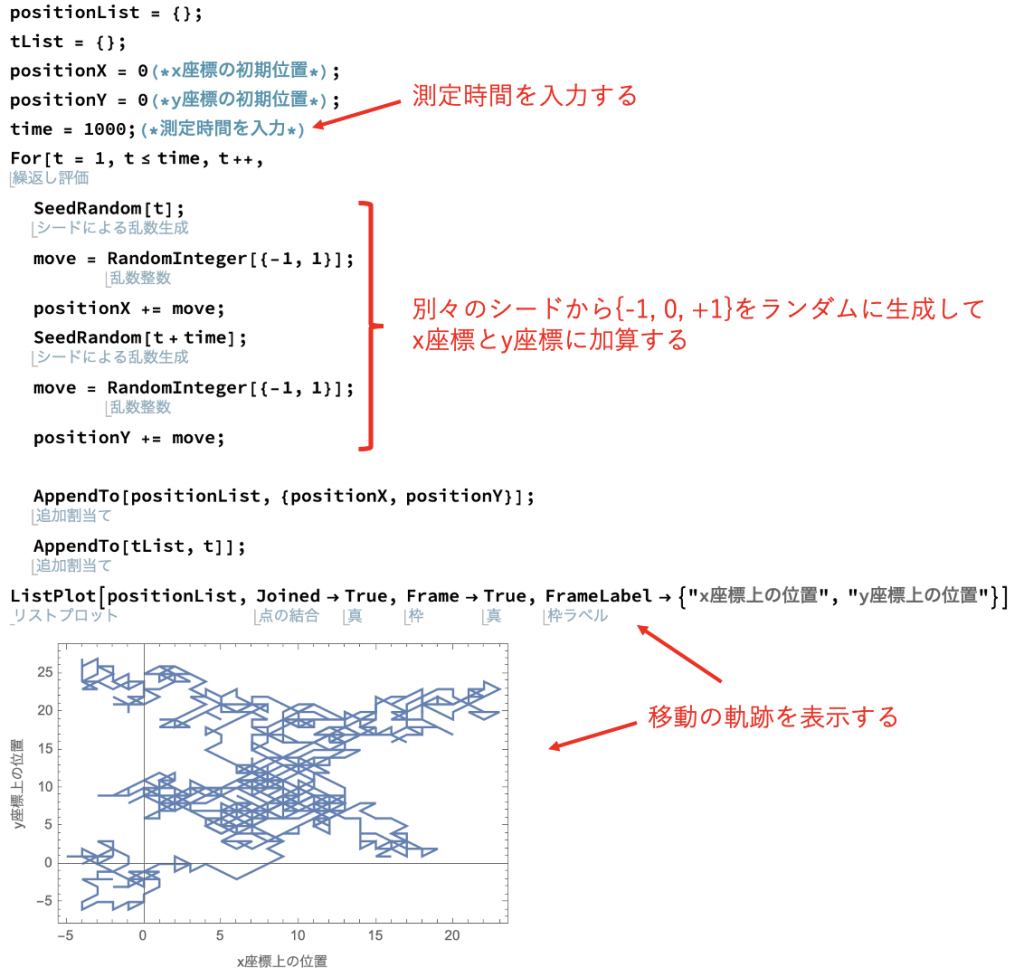
コピペ用は以下の通りです。
上記コードは、1秒毎に{-1, 0, +1}のどれかの数をx座標、y座標に加算していって、その時系列変化をグラフで表示したものになります。
注意点としましては、x座標、y座標には別々のシードから生成した乱数を使用している点です。x座標はシードに「t」、y座標はシードに「t + time」を使用することで、異なるシードから乱数が生成されるようになっています。
さて、次は先程と同様の解析を行ってみましょう。
つまり、今作成したxy座標のリストをもとにして時間tに対するMSDのプロットを作成してみましょう。
私が作成したコードは以下の通りです。
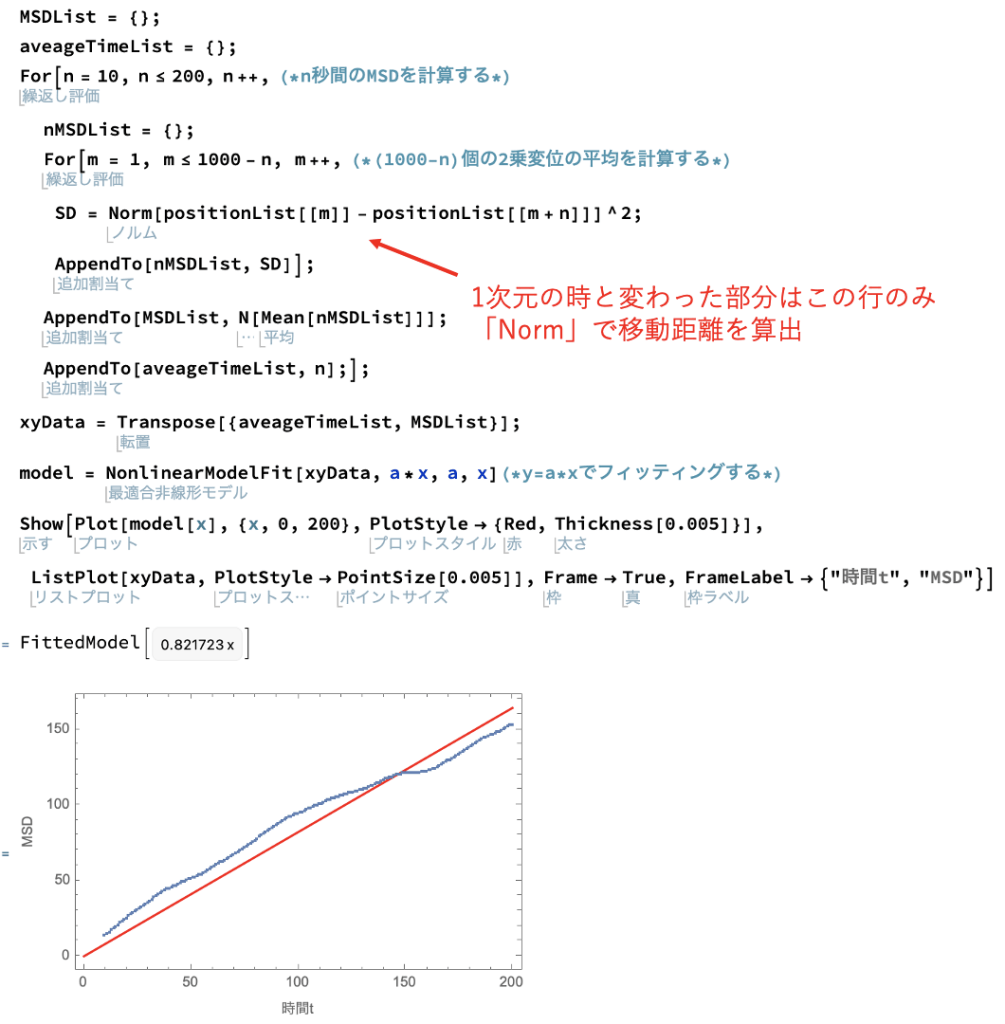
コピペ用は以下の通りです。
上記コードは、7行目以外は1次元の場合と同じコードです。
7行目では移動距離を算出するためにベクトルの長さを返す関数である「Norm」を使用しています。
(終点と始点の位置ベクトルを引き算して作ったベクトルの長さは、始点と終点の距離を表します)
「Norm」によって計算された移動距離を2乗して平均を取ることでMSDが計算されます。
そして「t = 10」から「t = 200」までのMSDのプロットとその線形フィッティング関数を1つのグラフにまとめて表示しています。
このグラフをみると確かにMSDは時間に比例していそうですね。
ちなみに先程と同様に線形フィッティング関数の傾きは拡散係数と関連しています。
以上で2次元のランダムウォークシミュレーションの実装が完了しました。
おわりに
以上をもって第6回の「乱数シミュレーション」を終了します。
今回題材として扱った「ランダムウォークシミュレーション」は、物理や化学、生物をはじめとして金融や経済の分野でも頻繁に登場します。
しかしながら、今回特に新しいテクニックを使用することなく「ランダムウォークシミュレーション」を実装することができました。
つまり、ここまで根気よく講座をお読みいただいた方は、既にMathematicaの基礎は十分身に付いていると思います。
そこで「超初心者向けMathematica講座」は次回で最終回とします。
最終回である第7回では「機械学習」について解説いたします。
それではお疲れ様でした。
